十字交叉法主要解決的就是比值的混合問題，在事業(yè)單位考試的過程中，資料分析部分解題經(jīng)常用的一種解題方法。它應用起來快速、準確、方便，為我們考試中秒殺題目提供了很大的助力。那么接下來國家事業(yè)單位考試網(wǎng)（www.linusblanket.net）跟大家一起來學習十字交叉法。

　　一、十字交叉法概述

　　十字交叉法是解決比值混合問題的一種非常簡便的方法。這里需要大家理解“比值”“混合”這兩個概念。比值：滿足C/D的形式都可以看成是比值；混合：分子分母具有可加和性。

　　平均數(shù)問題、濃度問題、利潤問題、增長率問題、比重等混合問題，都可以用十字交叉法來解決。

　　二、十字交叉法的模型：

 

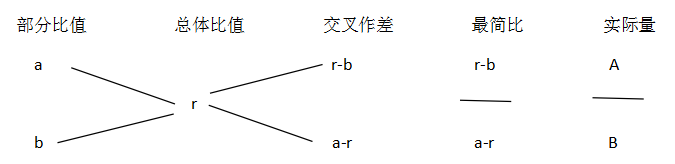
　　在該模型中，需要大家掌握以下幾個知識點：

　　1、a和b為部分比值、r為整體比值、A和B為實際量

　　2、交叉作差時一定要用大數(shù)減去小數(shù)，保證差值是一個正數(shù)，避免出現(xiàn)錯誤。這里假定a>b

　　3、實際量與部分比值的關系

　　實際量對應的是部分比值實際意義的分母。如：平均分=總分/人數(shù)，實際量對應的就是相應的人數(shù)；濃度=溶質/溶液，實際量對應的就是相應的溶液質量；增長率=增長量/基期值，實際量對應的就是相應的基期值。

　　4、在這里邊有三組計算關系

　　(1)第一列和第二列交叉作差等于第三列

　　(2)第三列、第四列、第五列的比值相等

　　(3)第1列的差等于第三列的和

　　三組計算關系是我們應用十字交叉法解題的關鍵，一定要記住并且靈活應用。

　　三、四種考查題型

　　1、求a，即已知總體比值、第二部分比值、實際量之比，求第一部分比值。

　　例 某班有女生30人，男生20人。期中的數(shù)學考試成績如下，全班總的平均分為76，其中男生的平均分為70。求全班女生的平均分為多少?

　　解析：平均分=總分/人數(shù)，是比值的形式。此題中，男生的平均分和女生的平均分混合成了全班的平均分，是比值的混合問題，可以用十字交叉法來解題。

 

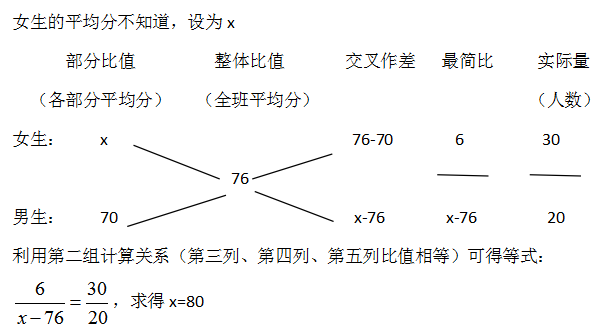
　　2、求b，即已知總體比值、第一部分比值、實際量之比，求第二部分比值。

　　例 某班有女生30人，男生20人。期中的數(shù)學考試成績如下，全班總的平均分為76，其中女生的平均分為80。求全班男生的平均分為多少?

　　解析：平均分=總分/人數(shù)，是比值的形式。此題中，男生的平均分和女生的平均分混合成了全班的平均分，是比值的混合問題，可以用十字交叉法來解題。

 

　　3、求r，即已知第一部分比值、第二部分比值、實際量之比，求整體比值。

　　例 某班有女生30人，男生20人。期中的數(shù)學考試成績如下女生的平均分為80，男生的平均分為70。求全班的平均分為多少?

　　解析：平均分=總分/人數(shù)，是比值的形式。此題中，男生的平均分和女生的平均分混合成了全班的平均分，是比值的混合問題，可以用十字交叉法來解題。

 

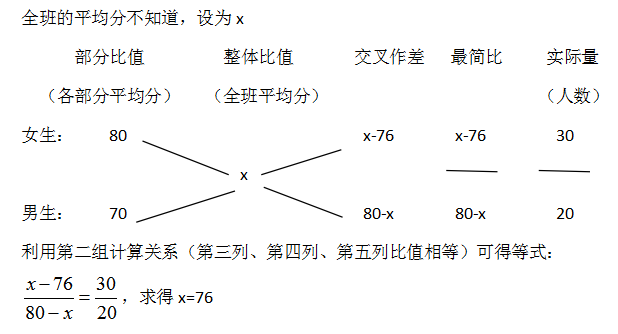
　　4、求實際量之比，即已知第一部分比值、第二部分比值、整體比值，求實際量之比。

　　例 某班期中的數(shù)學考試成績如下：全班平均分為76，女生的平均分為80，男生的平均分為70。求班級中女生與男生的人數(shù)之比?

　　解析：平均分=總分/人數(shù)，是比值的形式。此題中，男生的平均分和女生的平均分混合成了全班的平均分，是比值的混合問題，可以用十字交叉法來解題。

 

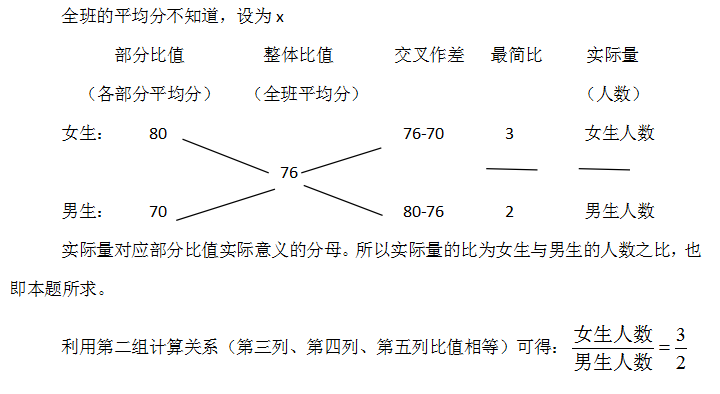
　　再利用十字交叉法解決問題時，需要深刻理解模型中的每個概念以及相關的計算關系和注意的點。小編希望大家能夠靈活運用并且能在考試中快速解題。