職測答題技巧：幾何中的最短路徑問題
最短路徑問題考查形式通常為求點之間的最短距離，核心解題方法為平面上兩點之間，線段最短。在考試中最短路徑問題主要分為兩大類，平面幾何最短路徑與立體幾何最短路徑。雖然題目有多種問法，但萬變不離其宗，只要知識點掌握牢固、能夠融會貫通，無論如何創新如何結合，我們都可以熟練解決。
平面幾何最短路徑問題
1.兩點異側
題型特征：求在直線異側的兩點之間的最短距離，或在直線異側的兩點到第三點的最短距離之和
解題方法：兩點之間，線段最短，三點共線時距離之和最短
例1.【2011聯考】火車站A和B與初始發車站C的直線距離都等于akm，站點A在發車站C的北偏東20度，站點B在發車站C的南偏東40度，若在站點A和站點B之間架設火車軌道，則最短的距離為：
A. akm
B. 3akm
C. 2akm
D. 
akm
【解題思路】如圖所示，根據題意中A在C點北偏東20度和B在C點南偏東40度可知，A、B、C三點構成頂角為120度的等腰三角形，且AB為底邊。過點C做AB的中垂線，交AB于點D。根據勾股定理可得，C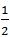D=
a，AD=
a，則AB=2AD=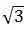
a，正確答案為D。
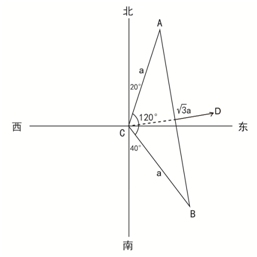
【點評】公務員考試中，三角形求邊長常用勾股定理和相似三角形。因此建議各位考生將常見三角形邊長比例熟練記憶，如30°直角三角形、等腰直角三角形、120°等腰三角形等。本題若變形為C火車站正東建立新火車站D，求AB兩點到D距離之和最短，因三點共線時距離之和最短，直接連接AB即為最短距離和。
2.兩點同側
題型特征：求在直線同側的兩點到第三點的最短距離之和
解題方法：將其中一點鏡像對稱，使三點共線
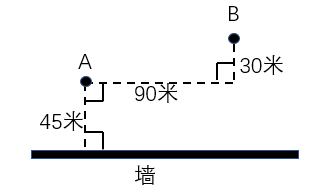
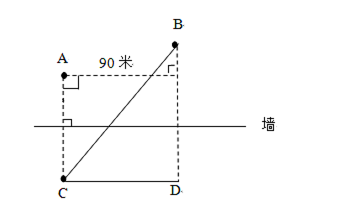
例1.【2019浙江】 A、B點和墻的位置如圖所示。現從A點出發以5米/秒的速度跑向墻，接觸到墻后再跑到B點。問最少要多少秒到達B點?
A. 30
B. 34
C. 38
D. 42
【解題思路】要用最短時間到達B點，在速度一定的情況下，需從A接觸到墻后再跑到B點所走的路程最短。如圖，由于A和B在墻的同側，可考慮做其中一個點關于墻的對稱點，該對稱點與另一個點的連線即為最短路程。假設做A點的對稱點C，最短距離為BC。CD=90米，BD=30+45+45=120米，最短距離BC=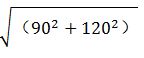
=150米，則t=
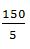=30秒,正確答案為A。
【點評】先判斷為同側問題，需要作其中一點的對稱點，再連接另外一點，用勾股定理求解。兩點同側時，對稱哪一個點都可以，但是一般為了計算方便，建議對稱短的那一個。
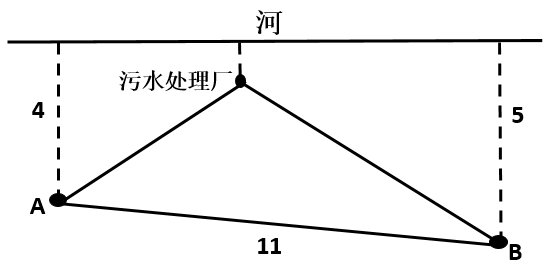
例2.【2017聯考】如下圖所示，某條河流一側有A.、B.兩家工廠，與河岸的距離分別為4km和5km，且A.與B.的直線距離為11km。為了處理這兩家工廠的污水，需要在距離河岸1km處建造一個污水處理廠，分別鋪設排污管道連接A.、B.兩家工廠。假定河岸是一條直線，則排污管道總長最短是：
A. 12km
B. 13km
C. 14km
D. 15km
【解題思路】如下圖所示，過污水處理廠做河岸的平行線HC，D為A關于HC的對稱點，則最短距離為DB，由題污水廠離河1km可得A點距離到HC為HA=HD=3km，B點距離HC等于EH=4km，則DE=3+4=7km。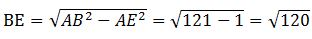
，所以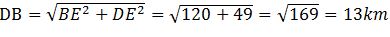
，正確答案為B。
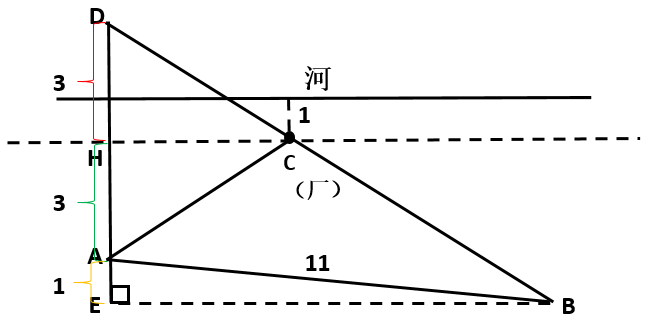
【點評】本題中題目AB為河流一側，因此為兩點同側。提醒大家注意，若以河為對稱軸，求的點為交點，此時污水處理廠建在河里，因此此題的對稱軸是第三個點所在的水平線，過C作一條沿河岸的平行線，軸距離河岸為1km。計算時若忽略了這一點，將無法求解正確答案。
立體幾何最短路徑問題
題型特征：求立體圖形中兩點的最短距離
解題方法：將立體圖形展開放在同一平面，連線計算
例1.【2019河北】長、寬、高分別為12cm、4cm、3cm的長方體ABCD-A_1 B_1 C_1 D_1上，有一個螞蟻從A出發沿長方體表面爬行到C_1獲取食物，其路程最小值是多少cm?
A. 13
B.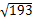
C.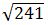
D. 17
由題干螞蟻從A出發沿長方體表面爬行到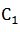
求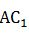
最短，畫圖可知，在長方體中A和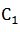不在同一平面，要求最短距離先要把A和C_1放在同一平面內，則把面
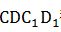翻折，形成面
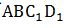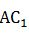，再連接，根據兩點之間直線最短求解。如下圖：
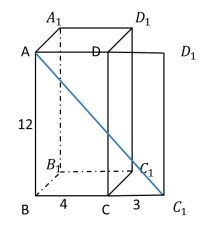
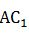是直角三角形ABC_1的斜邊，要讓斜邊最短，則兩直角邊的平方和要盡可能小。當AB=12，
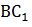=4+3=7時，兩直角邊的平方和最小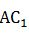，最短=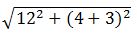
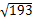=，正確答案為B。
【點評】長方體最短路徑問題可直接運用結論，長方體中相對的兩個頂點沿表面走的最短距離為：
；最短路徑數為2條，因為長方體存在對立面，每一條路徑都有一條與之相對的路徑，因此有2條。
例2. 【2013北京】A和B為正方體兩個相對的頂點，一個點從A出發沿正方體表面以最短路徑移動到B，則其可選擇的路線有幾條：
A. 2
B. 3
C. 6
D. 12
【解題思路】正方體有3組對立面，如圖可知每一條路線在對立面上都有一條與之對應的路線，因此每組對立面有2條路線，3組對立面共6條路線，正確答案為C。
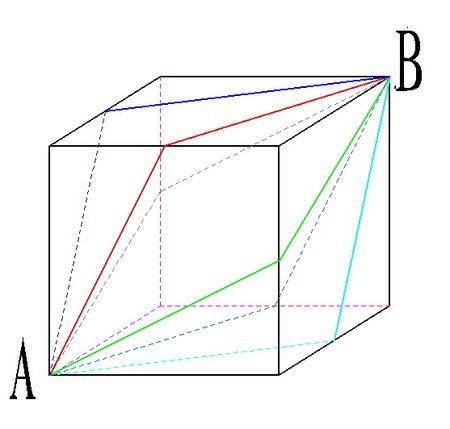
【點評】若本題為求A到B最短距離，則可將正方體展開，將AB放在同一平面內。連接AB后，AB=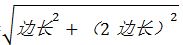
=
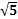邊長。
正方體最短路徑問題也有有對應結論，小編建議可以直接用結論做題，正方體中相對的兩個頂點最短距離為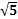邊長，最短路徑數為6條。
以上就是對于幾何中的最短路徑問題的詳細講解。
