職測(cè)數(shù)量關(guān)系：三者容斥問(wèn)題3個(gè)公式
容斥問(wèn)題本身存在包容與排斥的一種計(jì)數(shù)問(wèn)題，所以我們?cè)谔幚磉@一類(lèi)問(wèn)題的時(shí)候必須要注意扣除掉重復(fù)的部分，也要保證沒(méi)有遺漏，為了使重疊部分不被重復(fù)計(jì)算，人們研究出一種新的計(jì)數(shù)方法，這種方法的基本思想是：先不考慮重疊的情況，把包含于某內(nèi)容中的所有對(duì)象的數(shù)目先計(jì)算出來(lái)，然后再把計(jì)數(shù)時(shí)重復(fù)計(jì)算的數(shù)目排斥出去，使得計(jì)算的結(jié)果既無(wú)遺漏又無(wú)重復(fù)，這種計(jì)數(shù)的方法稱(chēng)為容斥原理。那我們接下來(lái)就來(lái)了解一下基于這種思想下的三者容斥問(wèn)題的計(jì)算公式。
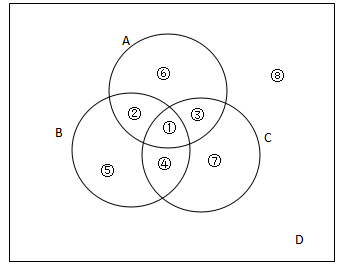
公式一：若條件給出A∩B，A∩C，B∩C，A∩B∩C的值
對(duì)于圖中的全集I來(lái)說(shuō)相當(dāng)于整個(gè)圖中所有部分之和，即I=A∪B∪C+D(D為非A非B非C的區(qū)域)，那么這里面我們算得A∪B∪C需要把其A,B,C中重復(fù)的區(qū)域扣除，如果我們把A,B,C加在一起，其中對(duì)于A∩B(①+②)的區(qū)域是在A,B中各參與計(jì)算一次，需要減一個(gè)A∩B，同樣的道理對(duì)于A∩C(①+③)，B∩C(①+④)均需要減去一個(gè)，對(duì)于重復(fù)的A∩B∩C(①)在我們把A.B.C加和時(shí)計(jì)算了三次，在減去A∩B，A∩C，B∩C均包含①區(qū)域則又減去三次，要保證沒(méi)有遺漏需要在加回一次A∩B∩C，則A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C。
公式總結(jié)：A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C
I=A∪B∪C+D=A+B+C-A∩B-A∩C-B∩C+A∩B∩C+D
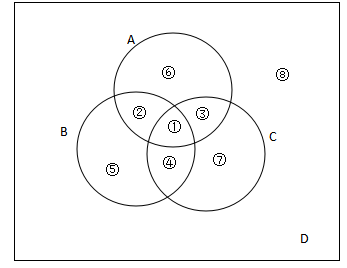
公式二：若條件給出包含兩種元素(②+③+④)和包含三種元素(①)的值
同樣的I=A∪B∪C+D，那么這里面我們算得A∪B∪C依舊需要把其A,B,C中重復(fù)的區(qū)域扣除，那么對(duì)于包含兩種元素(②+③+④)的區(qū)域，②在A,B中各加一次，重復(fù)一次;③在A,C中各加一次，重復(fù)一次;④在B,C中各加一次，重復(fù)一次,均重復(fù)一次，則需整體減去一倍的包含兩種元素(②+③+④)，對(duì)于重復(fù)的包含三種元素(①)在我們把A.B.C加和時(shí)計(jì)算了三次，則需要減去2倍的包含三種元素(①)，即A∪B∪C=A+B+C-含有兩種元素-2*含有三種元素
公式總結(jié)：A∪B∪C=A+B+C-含有兩種元素-2*含有三種元素
I=A∪B∪C+D=A+B+C-含有兩種元素-2*含有三種元素+D
【例題】某專(zhuān)業(yè)有若干學(xué)生，現(xiàn)開(kāi)設(shè)有甲、乙、丙三門(mén)選修課。有40人選修甲課程、36人選修乙課程、30人選修丙課程，兼選甲、乙課程的有28人、兼選甲、丙兩門(mén)課程的有26人、兼選乙、丙兩門(mén)課程的有24人、甲乙丙三門(mén)課程均選的有20人，三門(mén)課程均未選的有2人。該專(zhuān)業(yè)共有學(xué)生多少人?
A.48 B.50 C.52 D.54
解析：題目求解該專(zhuān)業(yè)共有多少名學(xué)生，即求解全集I，通過(guò)題目條件給出兼選甲、乙課程、兼選甲、丙兩門(mén)課程、兼選乙、丙兩門(mén)課程，兼選甲、乙、丙三門(mén)課程的人數(shù)，即給出條件A∩B，A∩C，B∩C，A∩B∩C的值，故選用公式一，則I=40+36+30-28-26-24+20+2
根據(jù)尾數(shù)為0選擇B。
我們?cè)趹?yīng)用容斥問(wèn)題時(shí)一定要注意到題目中所給出的條件，根據(jù)條件選取合適的公式計(jì)算。
