十字交叉法是數學運算、資料分析偶爾會用到的一種解題思路，運用它可以達到有效提速。“十字交叉法”，即通過十字圖對A/B=（r-b）/（a-r）進行簡化運算（令a＞b），如圖所示：

 

 

　　圖中的數學思路，不少同學在學生時代都接觸過，所以覺得很熟悉。“十字交叉法”實際上就是方程法的簡化，將運算思路用一種簡單的示意圖表示出來，簡化分析和計算過程，提高計算速度。

　　數量關系中如何迅速辨別考題是否適用十字交叉，做到快速套用解題？第一，它主要運用于經濟利潤、溶液問題、比值的混合問題等；第二，考題共同特征是“題干給出了兩個量和這兩個量的平均值，最后求兩個量的比例”。

 

　　這類問題就可以嘗試用“十字交叉法”解題，具體如何運用看幾道例題。

　　1.十字交叉法與溶液問題

 

　　【例題1】某項實驗，需要使用不同的A和B兩種氯化鈉溶液配制成濃度為15%的氯化鈉溶液，已知A溶液的濃度是B溶液的5倍，且若將50克A溶液和250克B溶液混合即可完成配置，那么A溶液的濃度是多少？

　　A、45%

　　B、40%

　　C、35%

　　D、30%

 

　　【特征分析】

　　根據題干可知，題干給出了A和B溶液的混合濃度（即A溶液濃度和B溶液濃度的平均值），且根據題干可知A的濃度和B的濃度，符合用十字交叉法的題干特征。

　　【解題思路】

　　A和B混合后的濃度為15%，混合前A溶液的濃度是B溶液的5倍，則假設B溶液的濃度為x%，則A溶液的濃度為5x%，混合后的濃度15%是總體比值，A和B溶液的濃度是部分比值，則根據十字交叉法可得：

 

 

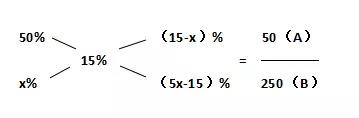
　　解得x=9，則A溶液的濃度為5×9=45，故答案為A。

　　2.十字交叉法與基本比值

　　【例題2】某單位為全體員工進行體檢，平均體重是57.5公斤，其中，男員工的平均體重為62.5公斤，女員工的平均體重為55.5公斤。則該單位的男、女員工的人數之比為：

　　A、2:5

　　B、2:7

　　C、7:2

　　D、5:2

 

　　【特征分析】

　　根據題干可知，題干給出男生平均體重和女生平均體重的兩個量，以及男女生的總體平均值，符合十字交叉法的題干特征。

　　【解題思路】

　　用十字交叉法進行解題，可得：

 

 

　　因此男、女員工的人數之比為2:5，故答案為A。

　　3.十字交叉法與經濟利潤

 

　　【例題3】某商店花10000元進了一批商品，按期望獲得相當于進價25%的利潤來定價。結果只銷售了商品總量的30%。為盡快完成資金周轉，商店決定打折銷售，這樣賣完全部商品后，虧本1000元，問商店是按定價打幾折？

　　A、九折

　　B、七五折

　　C、六折

　　D、四八折

 

　　【特征分析】

　　根據題干可知，賣出的30%按照25%的利潤來定價，賣出的70%按照利潤率為x%來定價，總虧損1000元可知總的利潤率為-10%，則該題符合十字交叉法的題干特征，可用十字交叉法解題。

　　【解題思路】

　　該商品的售價有兩種情況，一種是按25%的利潤來定價，一種是按打折后的售價，根據虧損了1000元可知利潤率為負的即1000/10000=-10%，假設打折后的利潤率為x%，按照25%的利潤定價的商品買了30%，則按照打折的利潤賣了70%，則：

 

 

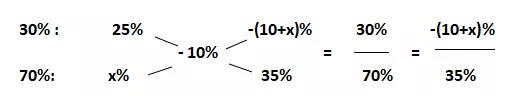
　　解得x=-25，則打折后的利潤率為-25%，假設商品的進價為100，則定價為100（1+25%）=125，打折后的售價為75元，則打的折扣為75÷125=0.6即六折。故答案為C。

 

　　以上，對于十字交叉法，第一次理解也許會有點困難，但實際上它的原理并不復雜，是一種基礎方法。它的運用非常靈活，適用于數學運算的多種題型，還有資料分析的“混合增長率”相關考題，也可以結合十字交叉法原理加以理解。

　　方法要能夠真正掌握，先要理解其原理，再是多加運用，所以，在復習的過程中要多多了解并盡可能掌握一些技巧，反復運用，考場上才更有可能“贏過時間”，達到事半功倍的效果哦！