職測資料分析:逆用比重增長破難題
來源:永岸公考
2024-11-13 10:40:08
相信大家對于職測資料分析的高頻考點——比重增長,它的判定、計算都不陌生吧。但是比重增長的逆向運用你會了嗎?今天帶大家首先回顧一下比重增長的知識點:
比重增量的公式
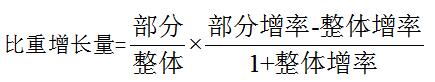
比重變化判定依據
部分增率>整體增率,現期比重>基期比重
部分增率<整體增率,現期比重<基期比重
部分增率=整體增率,現期比重=基期比重
一、比重變化的逆運用
如果問:某年-某年,A的增速超過B 的增速的年份有幾年?而材料并未給定這幾年A與B的增速,但給了比重,此時根據材料已知現期比重與基期比重的大小,從而逆向判定增速的大小,這就是比重變化的逆向運用!
【例題1】
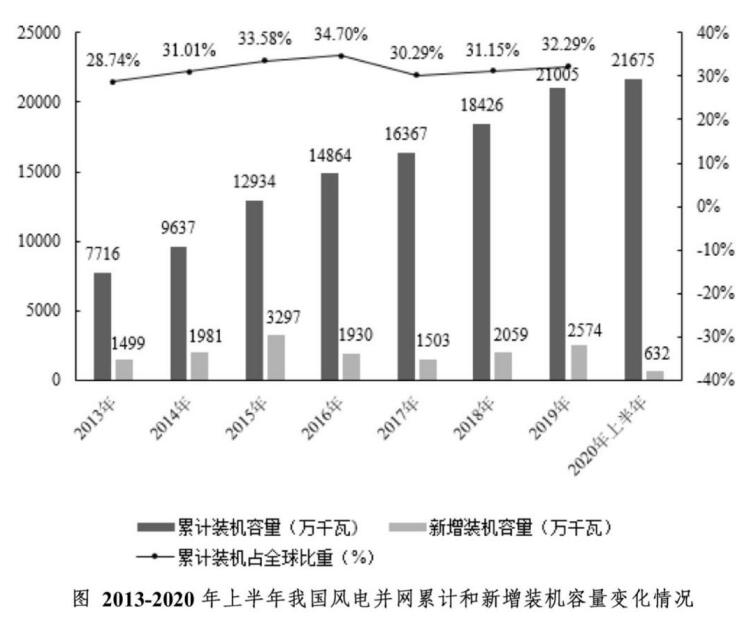
問題:2014-2019年,我國風電并網累計裝機容量的同比增速超過全球的有( )年。
A.3
B.4
C.5
D.6
【技巧點撥】問法求:風電增速>全球增速,材料沒有這兩個指標的增速,但我們已知14年-19年風電占全球的比重,可根據比重變化的判定逆推增速的大小關系!
答案:C
【解析】根據比重變化的判定可知,想要部分增率>整體增率,必須滿足現期比重>基期比重。折線圖可知2014年風電占全球的比重(31.01%)大于2013年的比重(28.74%);2015年風電占全球的比重(33.58%)大于2014年的比重(31.01%);2016年風電占全球的比重(34.7%)大于2015年的比重(33.58%);2018年風電占全球的比重(31.15%)大于2017年的比重(30.29%);2019年風電占全球的比重(32.29%)大于2018年的比重(31.15%);共計2014年-2016、2018年和2019年5個年份,故而選擇C。
二、比重增量的逆運用
如果材料給定兩期比重數值或比重的增量,求部分的增速或整體增速時,我們就需要將已知量代入公式,從而逆向求解,這就是比重增量的逆運用!
【例題2】2021年G省前三季度全省地區生產總值13985.53億元,比上年同期增長8.7%,比2019年同期增長12.2%從財政收入看,前三季度,全省一般公共預算收入中稅收收入887.74億元,增長13.8%,占一般公共預算收入的比重為63.5%,占比較上年同期提高1.8個百分點。
問題:2021年G省前三季度一般公共預算收入的同比增速約為:
A.10.6%
B.12.1%
C.13.9%
D.15.2%
【技巧點撥】問法求:21年前三季度一般公共預算的增速,材料已知稅收收入的占比以及比重的增量,可根據比重增量的公式,代入已知量逆推增速!
答案:A
【解析】部分是:稅收收入,整體是:一般公共預算收入。定位材料:2021年前三季度全省一般公共預算收入中稅收收入887.74億元,增長13.8%,占一般公共預算收入的比重為63.5%,占比較上年同期提高1.8個百分點。第一步:部分增率為13.8%,整體增率為x%;由于比重增量為正,能推出部分增率>整體增率,即13.8%>x%,排除C、D。第二步:比重增量<|部分增率-整體增率|,即1.8%<|13.8%-x%|,可得x%<12%,排除B;故而選擇A。
【例題3】2014年,某省全社會研發經費達122.13億元,研發經費占GDP的比重達0.68%,比2013年下降0.02個百分點。
問題:若2014年該省GDP同比增速為7.8%,則當年該省全社會研發經費同比增速為( )。
A.1%
B.5%
C.10%
D.18%
【技巧點撥】問法求:14年全社會研發經費的增速,材料已知研發經費占GDP的比重及比重增量,可根據比重增量的公式,代入已知量逆推增速!
答案:B
【解析】部分是:研發經費,整體是:GDP。定位材料:研發經費占GDP的比重達0.68%,比2013年下降0.02個百分點,GDP同比增速為7.8%。第一步:部分增率為x%,整體增率為7.8%;由于比重增量為負,能推出部分增率<整體增率,即x%<7.8%,排除C、D。第二步:比重增量<|部分增率-整體增率|,即0.02%<|x%-7.8%|,可得x%<7.78%,無法排除,代入公式逆向推導,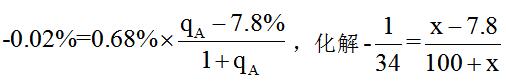 解出x≈4.8,選到B。
解出x≈4.8,選到B。
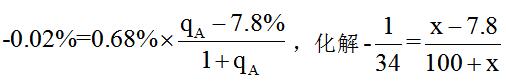 解出x≈4.8,選到B。
解出x≈4.8,選到B。
免費學習資源(關注可獲取最新開課信息)







